SSReflect methodology

What is SSReflect

• A software package
• A tactic language
• A proof methodology

SSReflect package

• Part of Mathcomp library (95 kLoC)
• SSReflect's size is 22kLoC
• Can be used as an stdlib overlay

SSReflect package

• $ opam install coq-mathcomp-ssreflect
  

• natural numbers
• sequences (lists)

• types with decidable equality
• types with decidable order
• lattices

• tuples (length-indexed lists)
• finite types, sets, functions
• …

SSReflect language

Sample proof:

Lemma drop_nseq i j x :
  drop i (nseq j x) = nseq (j - i) x.
Proof.
case:(leqP i j)=> [/subnKC {1}<-|/ltnW j_le_i].
- by rewrite nseqD drop_size_cat // size_nseq.
by rewrite drop_oversize
     ?size_nseq // (eqP j_le_i).
Qed.

SSReflect language

• Implemented as a Coq plugin
• Supports SSReflect proof methodology
• Proof language of Mathcomp and its ecosystem

• Extends and changes some defaults of Gallina and redefines some vanilla tactics
• Compatible with "vanilla" tactics

SSReflect language

• Precise bookkeeping
• No autonaming of assumptions – lead to fragile proofs
• Control the size of the proof context

SSReflect language

• Implemented as tacticals and easily integrated into the main story of the proof
• The goal can be thought of as a stack of quantified variables and assumptions as in concatenative languages
• Tactics act on the top of the stack

SSReflect proof methodology

• Aimed at formalization of finite objects in type theory
• Based on the pervasive use of computation with symbolic representations
• Statements explicitly contain symbolic representations mixed with logical ones

Large-scale reflection

• Large scale: e.g. ring tactic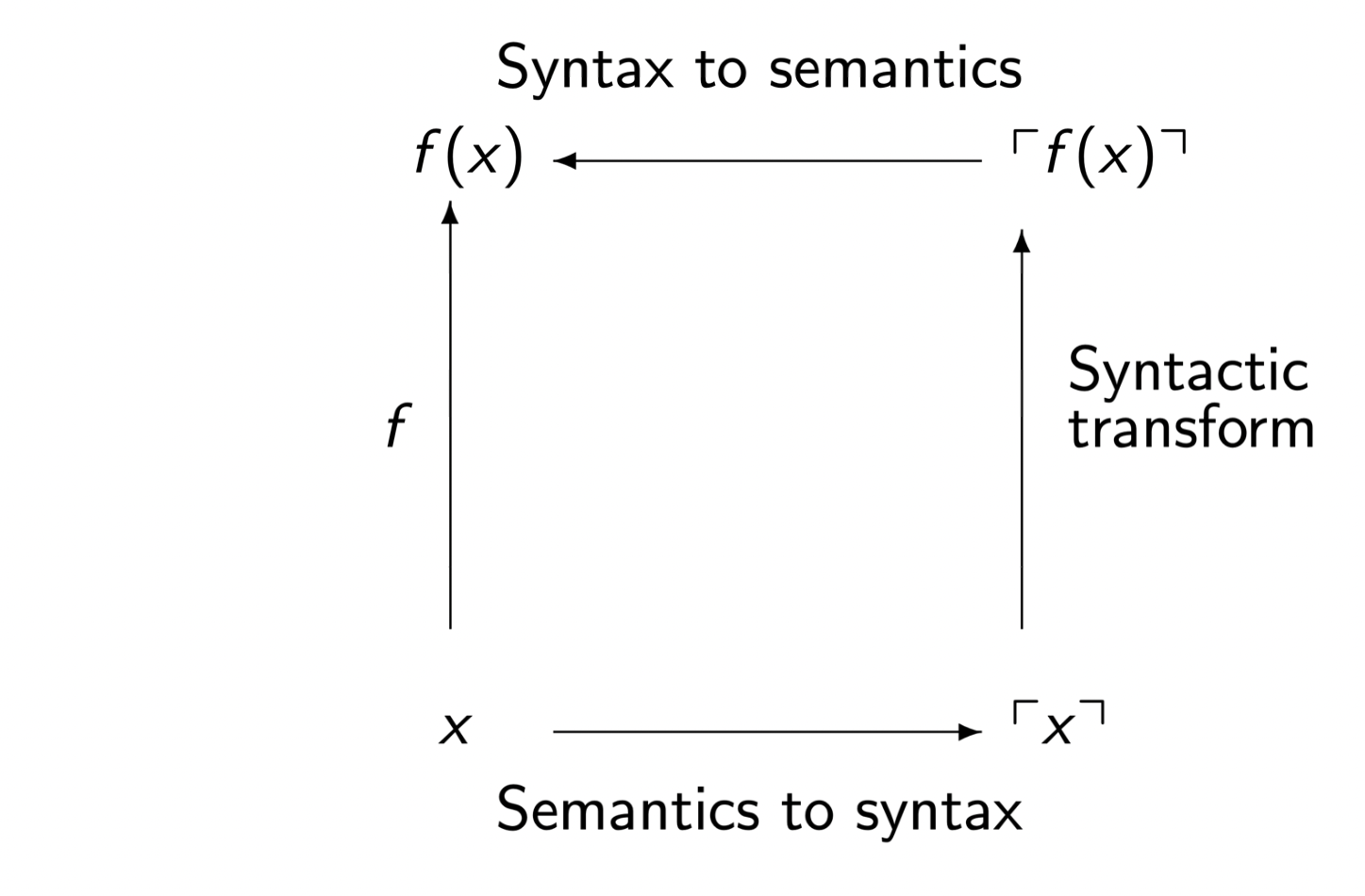

  

Small-scale reflection

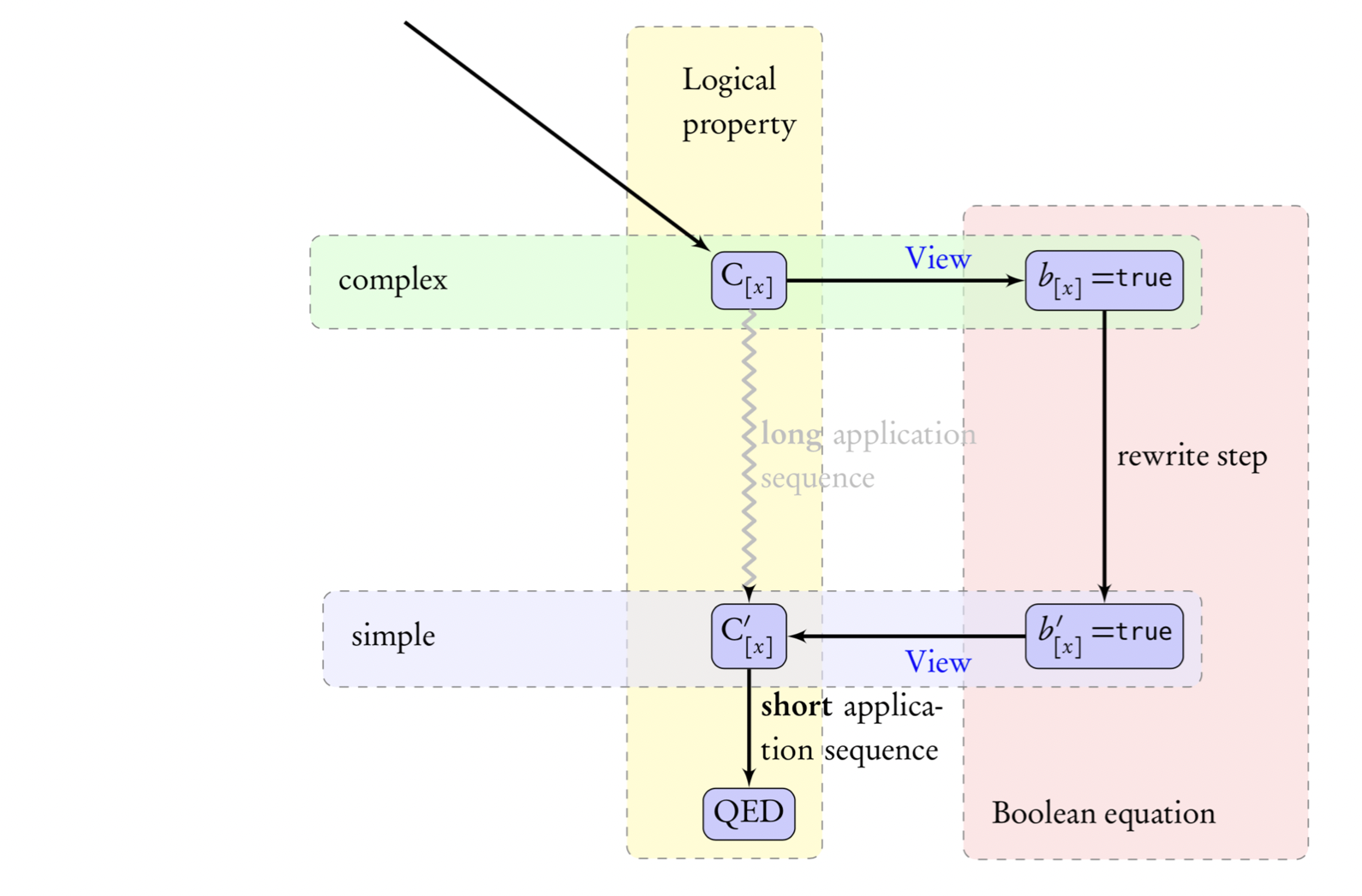
SSReflect proof methodology

• Translation between logical and symbolic representations is made explicit with the proof script
• The user directs partial evaluation which serves as a local form of proof automation

Prop vs bool

• Connectives in Prop are types: natural deduction
• Connectives in bool are functions: brute-force evaluation
• SSReflect lets you use the best of both worlds

SSReflect motto

"If a predicate is decidable, it should be defined as a boolean predicate!"